Research

Derivative-Informed Neural Operators

For DINO related work, please see my DINO page.

Stochastic Optimization

Some of my research focuses on efficient and scalable methods for the solution of stochastic and finite-sum minimization problems, stated below for unconstrained problems.

\[\text{(Stochastic)} \quad \min_w f(w) = \mathbb{E}_{\zeta \sim \pi}\left[F(w,\zeta) \right]\] \[\text{(Finite-Sum)} \quad \min_w f(w) = \frac{1}{N}\sum_{i=1}^N F_i(w)\]

Hessian-Averaging

With my collaborator Raghu Bollapragada, we have developed efficient subsampled methods allowing both Hessian and gradient inexactness for the solution of stochastic and finite-sum minimization problems. The iterate update is of the form

\[w_{k+1} = w_k - \alpha_k H^{-1}_k g_k\]

where \(H_k\) and \(g_k\) are Hessian and gradient approximations, and \(\alpha_k\) is the step size.

In these methods the per-iteration computational costs associated with the subsampled Hessian computations do not increase. The variance in the Hessian operator is controlled instead by using averaging of past iterates

\[\widehat{H}_k = \sum_{i=0}^k \gamma_i \nabla^2 F_{S_i}(w),\]

where \(S_i\) is an index set used in subsampled approximations of the Hessian at each iteration, and \(\gamma_i \in(0,1)\) with \(\sum\limits_{i=0}^k \gamma_i = 1\).

This approach concentrates the Hessian error asymptotically, leading to local superlinear convergence, with rates summarized below.

	Stochastic	Finite-sum
Na et al.	\(\mathcal{O}\left(\frac{\log k}{\sqrt{k}}\right)\)	\(\mathcal{O}\left(\frac{\log k}{\sqrt{k}}\right)\)
Our preprint	\(\mathcal{O}\left(\frac{1}{\sqrt{k}}\right)\)	\(\mathcal{O}\left(\frac{1}{k}\right)\)

In our work we allow for gradient inexactness using subsampled gradients where the sample sizes are chosen adaptively ensuring asymptotic exactness.

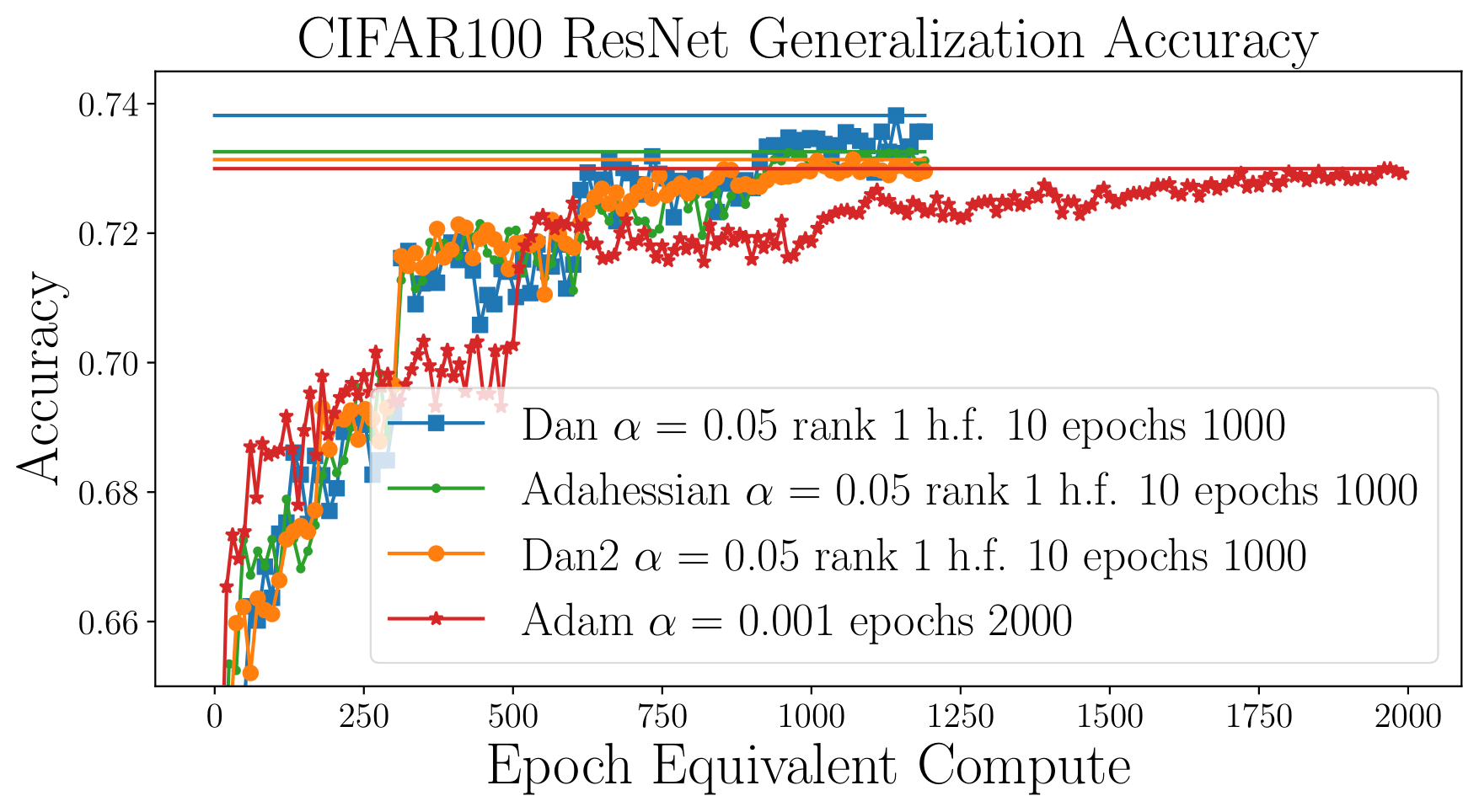
We propose the efficient practical algorithm Diagonally-averaged Newton, which utilizes diagonally averaging of the Hessian. We achieve state-of-the-art practical performance on challenging machine learning classification problems.

\(\infty\)–IDIC

Led by UT ME PhD student Joseph Kirchhoff, we have developed \(\infty\)–IDIC, an infinite-dimensionally consistent formulation of integrated digital image correlation (DIC). This formulation allows us to devise scalable and efficient algorithms to determine heterogeneous fields that parametrize PDEs given image data of their deformations.

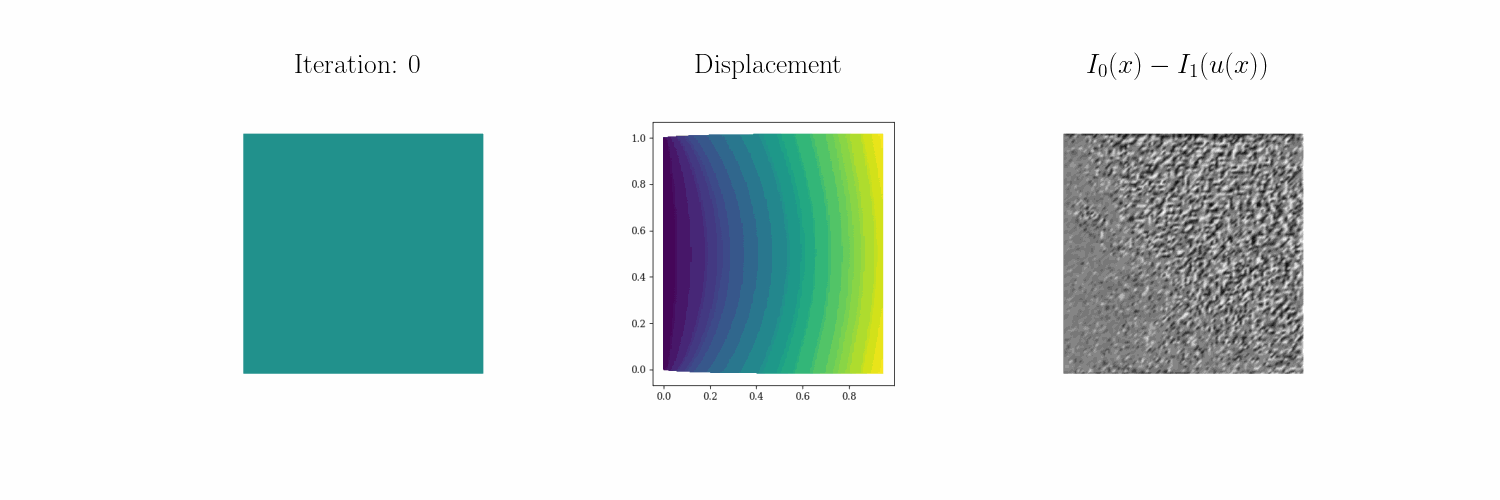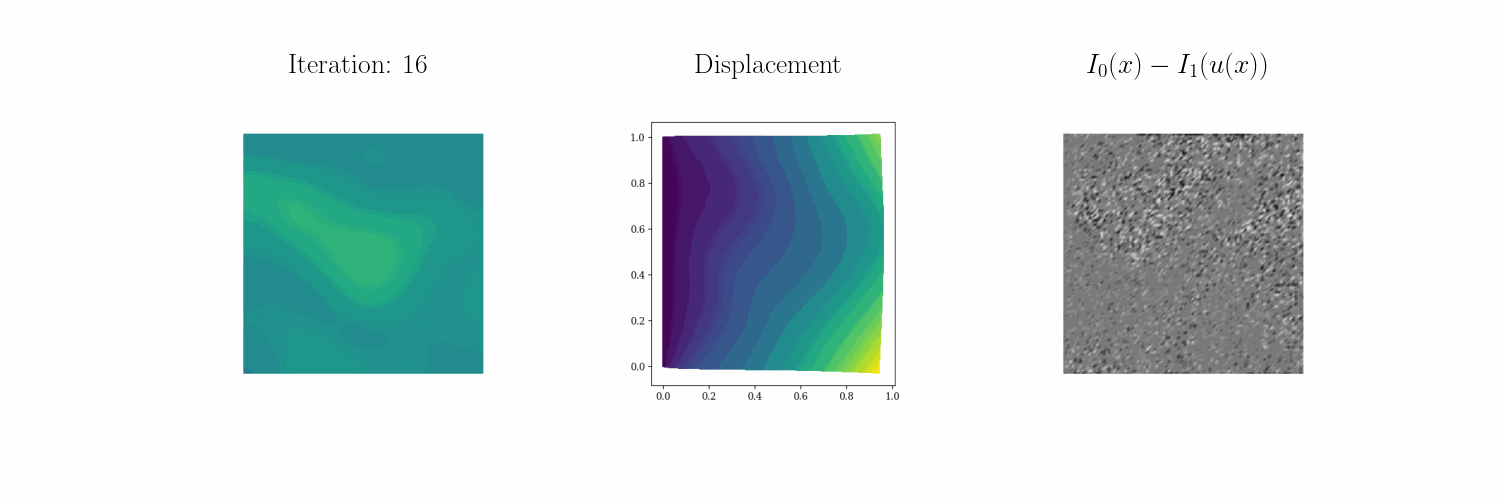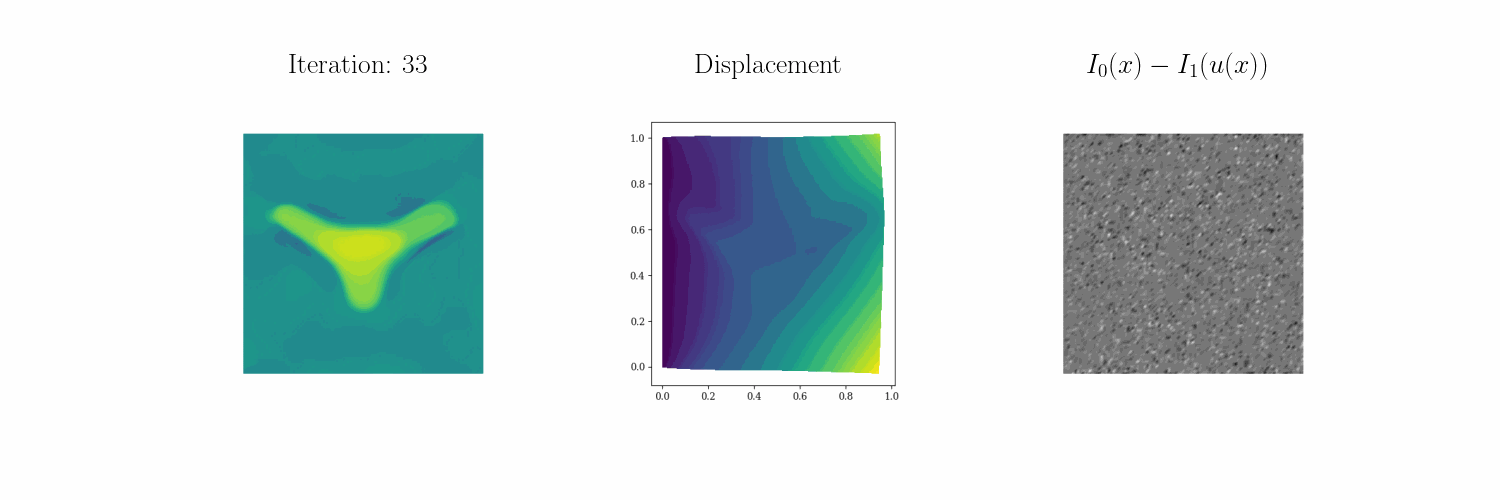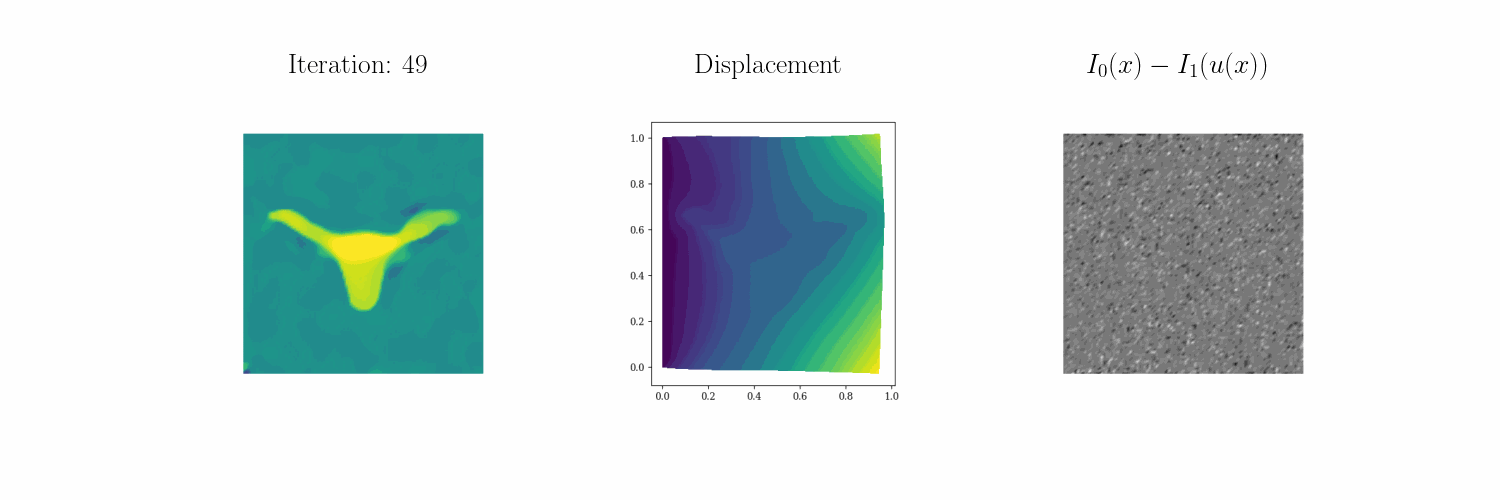
For example, we seek to characterize the properties of elastic solids from static loading tests. For more information see our preprint and our technology page. Below you can see how \(\infty\)–IDIC can invert for a Bevo-shaped elastic modulus profile from four different static loading tests:

Compression

Tension

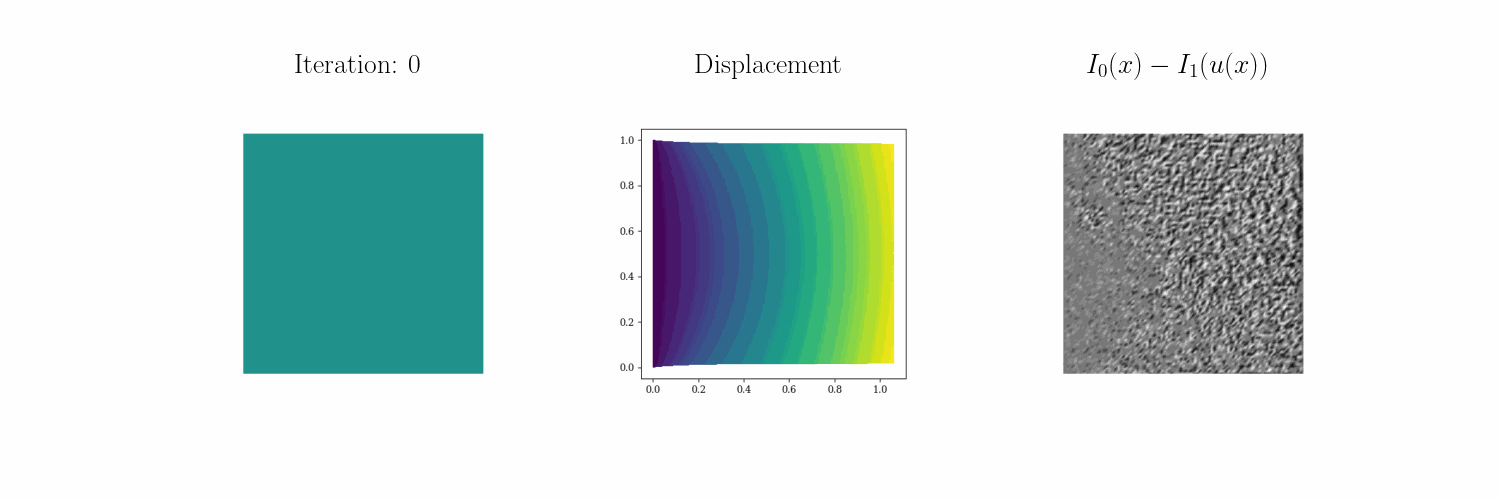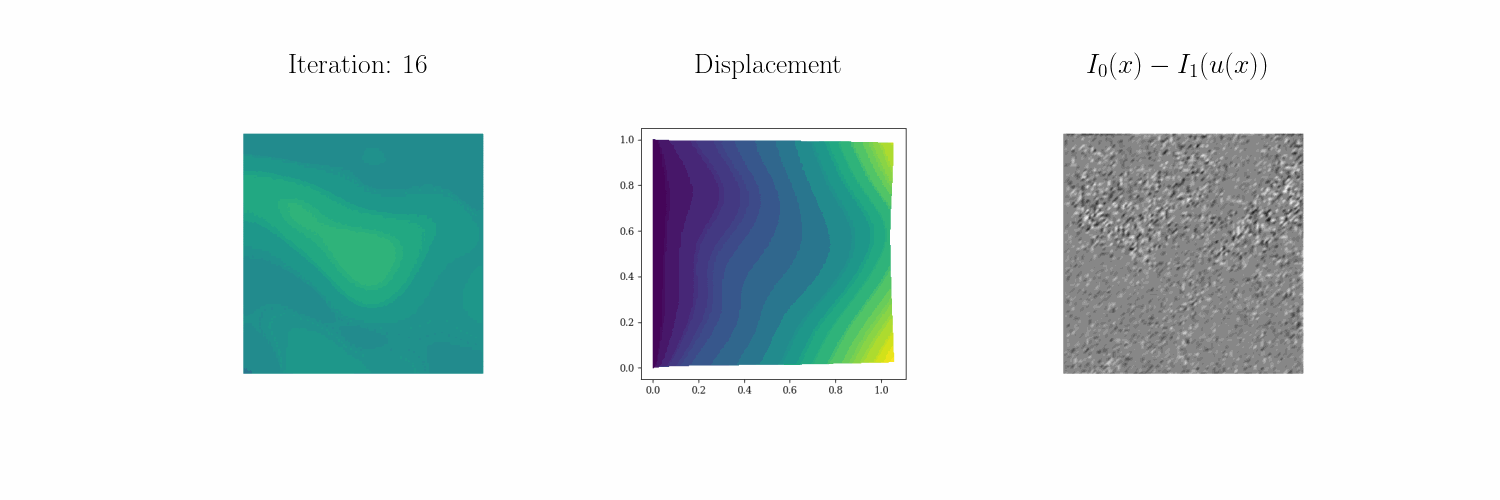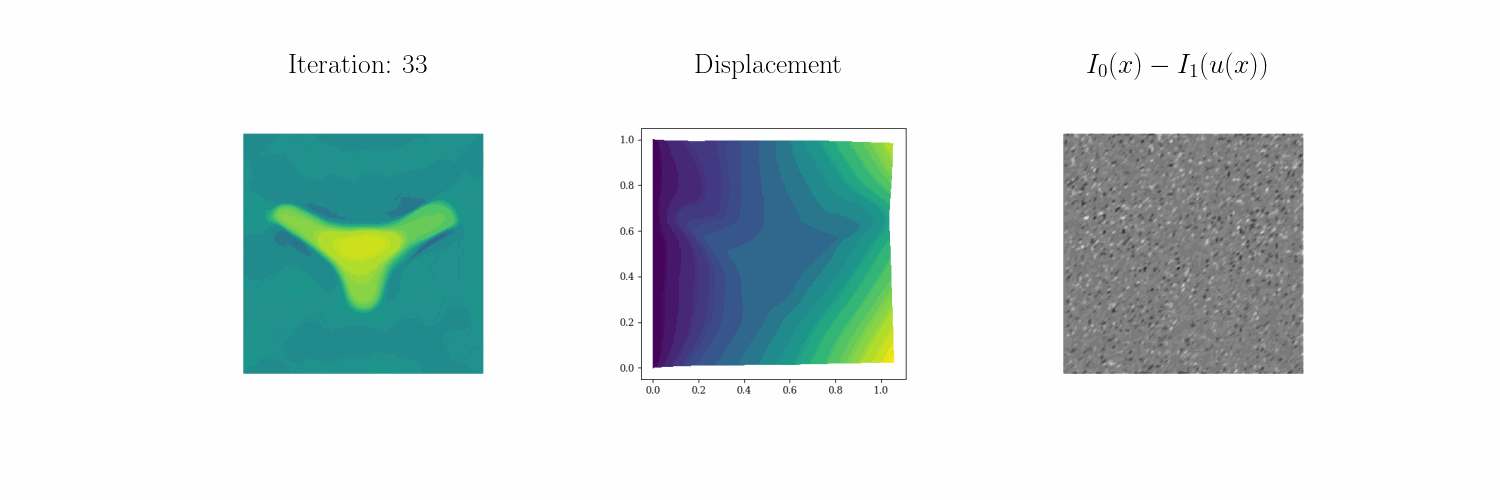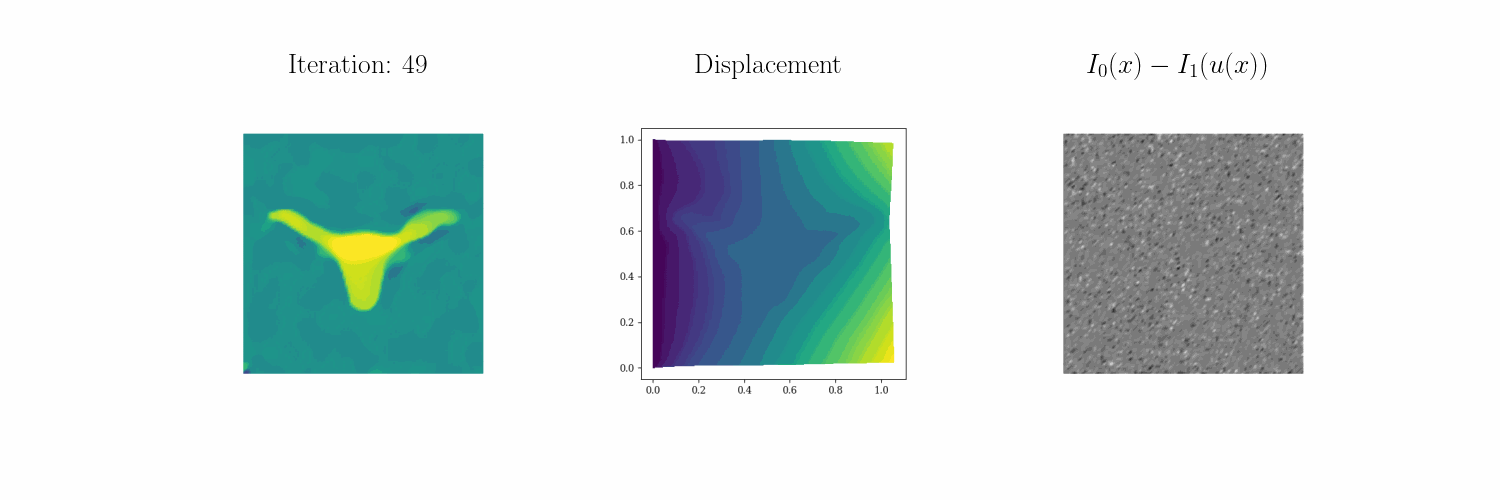
Bending down

Bending up